Berechnung und Interpretation von Verteilungen
Wir haben jetzt eine Menge verschiedener Methoden kennengelernt, mit denen wir uns einen Eindruck davon machen können, wie unsere Daten verteilt sind. Um den Begriff der Verteilung an sich haben wir dagegen bis hierher einen Bogen gemacht. Dabei spielt die Art der Verteilung für viele weiterführende Anwendungen eine große Rolle. Manche statistische Verfahren setzen spezifische Verteilungen voraus.
Statistische Verteilungen stellen eine Verbindung her zwischen den empirisch gewonnenen Daten und auf Wahrscheinlichkeit basierenden Aussagen, die wir daraus ableiten wollen. Dabei steht die Frage im Zentrum, mit welcher Wahrscheinlichkeit ein bestimmtes Zufallsereignis eintritt bzw. wie wahrscheinlich es ist, dass eine zufällig gezogene Stichprobe so ausfällt, wie es beobachtet wurde. Können wir annehmen, dass ein Merkmal auf eine bestimmte Weise verteilt ist, können wir eine Prognose abgeben, in welchem Rahmen eine Stichprobe liegen wird. Interessant wird es insbesondere dann, wenn sich nachher zeigt, dass die theoretische Schätzung falsch war und völlig andere Ergebnisse herauskommen. Denn das bedeutet, dass unsere Daten von Faktoren beeinflusst werden, die wir nicht mit eingerechnet haben.
Wir hätten also gerne eine Funktion, die es uns ermöglicht, alle denkbaren Stichproben auf einen Wahrscheinlichkeitswert zwischen 0 und 1 abzubilden. Wenn abzählbar viele Ereignisse eintreten können (z.B. beim Würfeln oder Münzwurf), spricht man von Wahrscheinlichkeitsfunktionen. Bei stetigen Verteilungen (z.B. wenn Zeiträume betrachtet werden) verwendet man den Begriff Dichtefunktion. In beiden Fällen summieren sich alle Funktionswerte zu 1 auf. Eine kumulierte Wahrscheinlichkeits- bzw. Dichtefunktion nennt man Verteilungsfunktion. D.h. bei der Verteilungsfunktion werden die Funktionswerte der Wahrscheinlichkeits summiert bzw. die Dichtefunktion integriert.
Schauen wir uns als Beispiel das Histogramm der Allbus-Einkommensverteilung aus den vorherigen Abschnitten an.
1 Data Management
Dazu laden wir zunächst die Daten und berechnen einige Parameter:
2 Berechnung von arithmetischem Mittel, Median, Modus und Standardabweichung
mean_einkommen = mean(allbus_df$Einkommen)
median_einkommen = median(allbus_df$Einkommen)
modus_einkommen = get_mode(allbus_df$Einkommen)
sd(allbus_df$Einkommen)[1] 1609.459Wir plotten zunächst unsere Lageparameter im Histogramm:
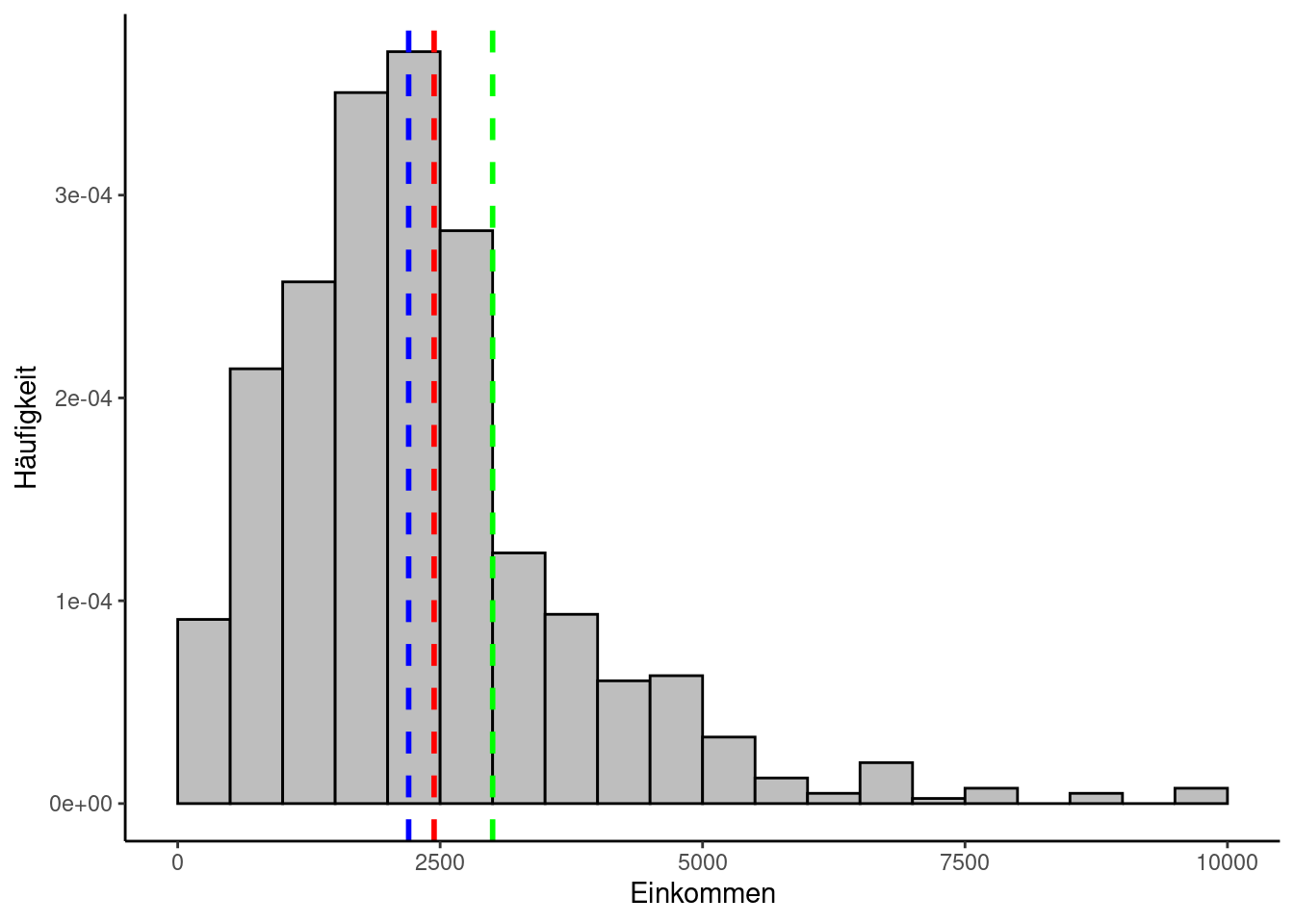
Zunächst einmal sieht man, dass sich die Messwerte in einem bestimmten Bereich häufen und eine zumindest annähernde Glockenform aufweisen. Der höchste Punkt deckt sich in etwa mit dem Mittelwert, hier vor allem dem Median (blau) und dem arithmetischen Mittel (rot), während der Modus (grün) etwas abseits liegt. Sie verteilen sich nicht gleichmäßig, was bei Einkommensdaten auch nicht zu erwarten gewesen wäre. So ganz symmetrisch sieht die Verteilung aber auch nicht aus, sondern wirkt etwas nach links gequetscht. Man nennt das auch “rechtsschief” bzw. “linkssteil”. Ein Indiz hierfür ist auch, dass das arithmetische Mittel größer ist als der Median. Das nach rechts gequetschte Gegenstück hieße “linksschief” bzw. “rechtssteil”. Diese Asymmetrie ist auch dadurch bedingt, dass ein erheblicher Teil der Studienteilnehmenden im Datensatz nicht vorkommt. Leute, die keine Angabe gemacht oder angegeben haben, dass sie über kein eigenes Einkommen verfügen, wurden beim Laden herausgefiltert. Die annähernde Glockenform stimmt jedoch hoffnungsvoll, dass der Datensatz mit einer Verteilung zusammenhängt, die in der Statistik von besonderer Bedeutung ist und die wir im Folgenden genauer betrachten werden: Die Normalverteilung.
3 Die Normalverteilung
Diese Verteilung ist auch ihrer charakteristischen Form wegen als Glockenkurve oder nach ihrem maßgeblichen Entdecker Carl Friedrich Gauß als Gauß-Verteilung bekannt. Relativ viele andere Verteilungen lassen sich bei ausreichend großer Stichprobengröße mit der Normalverteilung approximieren. Sie ist symmetrisch und der Mittelwert ist ihr Maximum.
Ca. 68% der Werte liegen innerhalb einer Standardabweichung vom Mittelwert entfernt, ca. 95% innerhalb von zwei Standardabweichungen und ca. 99,7%, also fast alle, innerhalb von drei Standardabweichungen.
Die Dichtefunktion der Normalverteilung wird folgendermaßen berechnet:
\[ f(x,\mu,\sigma) = \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^{-\frac{(x-\mu)^2}{2 \sigma^2}} \]
Dabei ist \(\mu\) der Mittelwert (arithm. Mittel, Median, oder Modus) und \(\sigma\) die Standardabweichung.
Bei einer Normalverteilung mit einem Mittelwert von null und einer Varianz von eins spricht man von einer Standardnormalverteilung:
\[ \phi(z) = f(z, 0, 1) = \frac{1}{\sqrt{2 \pi}} \cdot e^{- \frac{z^2}{2}} \]
Normal- aber nicht standardnormal verteilte Werte lassen sich leicht standardisieren, indem man den Mittelwert von ihnen abzieht und das Ergebnis durch die Standardabweichung teilt:
\[ z = \frac{Messwert - Mittelwert}{Standardabweichung} = \frac{x - \mu}{\sigma} \]
\(\mu\) kann dabei das arithmetische Mittel, der Median oder der Modus sein.
Der Vollständigkeit halber sei hier auch noch die Formel der Verteilungsfunktion aufgeschrieben:
\[ F(x, \mu, \sigma) = \frac{1}{2} \left[1 + \text{erf} \left (\frac{x - \mu}{\sigma \sqrt{2}} \right) \right] \]
\(erf\) steht für die Gauß’sche Fehlerfunktion.
Da R umfangreiche Funktionalitäten bereitstellt, um diese Verteilungen zu berechnen, ist es an dieser Stelle nicht notwendig, sich diese Formel einzuprägen oder irgendwas damit per Hand zu rechnen. R hat eine ganze Reihe an Verteilungen implementiert und stellt zu jeder davon u.a. vier Funktionen bereit:
- die Wahrscheinlichkeits-/Dichtefunktion, beginnend mit dem Buchstaben d,
- die Verteilungsfunktion, beginnend mit p,
- Quantile, beginnend mit q sowie
- Zufallszahlen auf Basis der jeweiligen Verteilung, beginnend mit r.
3.1 Visualisierung der Normalverteilung
Die folgenden vier Codebeispiele ergeben Visualisierungen der Normalverteilung bei unterschiedlichen Stichprobengrößen von \(n = 10\) bis \(n = 10000\). Dabei wird jeweils eine Zufallsstichprobe gezogen und die Verteilung der “Messwerte” als Histogramm ausgegeben. Je größer die Stichprobe, desto stärker sollte sich dabei die Verteilung der Zufallswerte der Dichtefunktion der Normalverteilung annähern, die hier rot dargestellt ist. Mittelwert und Standardabweichung sind so gewählt, dass die Standardnormalverteilung herauskommt. Wiederholen Sie die einzelnen Beispiele mehrmals, dann sollte jedesmal eine andere Stichproben-Verteilung herauskommen:
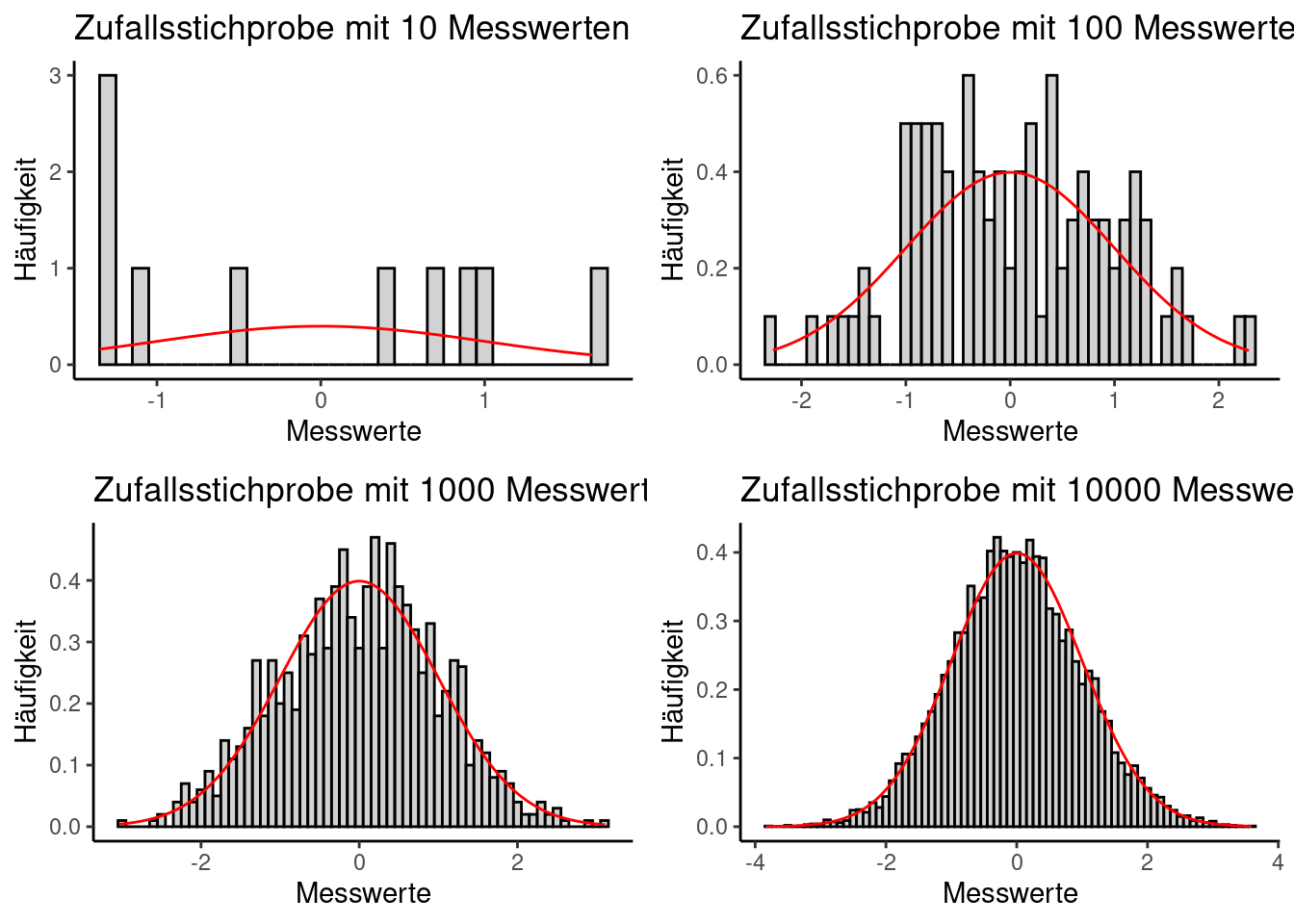
3.2 Interpretation der Normalverteilung
Aus der Visualisierung der unterschiedlichen Stichprobengrößen sollte ersichtlich geworden sein, warum ausreichend große Stichproben in der Statistik so wichtig sind. Erst ab einer ausreichend großen Anzahl Messwerten kann überhaupt sicher gesagt werden, ob die Daten einer bestimmten Verteilung folgen.
Wenn man weiß, dass ein bestimmtes Merkmal normalverteilt ist, kann man das nutzen, um mit relativ wenig Aufwand Berechnungen anzustellen. Angenommen, für unsere Einkommensdaten träfe das auch zu, dann könnte man z.B. mithilfe der Normalverteilung ausrechnen, wieviel Prozent der Population theoretisch über maximal 1500 Euro Netto-Einkommen im Monat verfügen. Dazu verwenden wir die Verteilungsfunktion der Normalverteilung, da wir an einem kumulierten Wert interessiert sind, nämlich allen möglichen Einkommenswerten bis maximal 1500 Euro. Wir übergeben der Funktion Mittelwert und Standardabweichung unserer Daten sowie die besagte Einkommensobergrenze:
income_mean = mean(allbus_df$Einkommen)
income_sd = sd(allbus_df$Einkommen)
income_median = median(allbus_df$Einkommen)
# Die Verteilungsfunktion der Normalverteilung: "p" + "norm":
pnorm(1500, mean=income_mean, sd=income_sd) [1] 0.2790626Wir bekommen als Ergebnis ca. 0.278. Das vergleichen wir mit dem 27,8%-Quantil unserer Messwerte:
Zur Erinnerung: Das 27,8%-Quantil teilt die untersten 27,8% vom Rest der Messwerte. Interessanterweise liegt die Grenze genau bei 1500 Euro, was exakt der Vorhersage entspricht. Die Übereinstimmung wird aber deutlich schwächer, wenn wir das mit dem (100-27,8)%-Quantil vergleichen:
Unsere Messwerte ergeben für das 72,2%-Quantil einen Wert von ca. 2977 Euro. Kalkulieren wir für das selbe Quantil bei der Normalverteilung das zu erwartende Einkommen, werden uns dagegen ca. 3393 Euro angegeben:
Die Datenlage weicht folglich um ca. 416 Euro von der theoretischen Annahme ab und fällt deutlich geringer aus. Ein Umstand, der sich auch grafisch widerspiegelt, wenn wir die Normalverteilung in unser Histogramm einzeichnen: Die blaue Kurve markiert den Median als Mittelwert, die rote das arithmetische Mittel, die gelbe das geometrische Mittel.
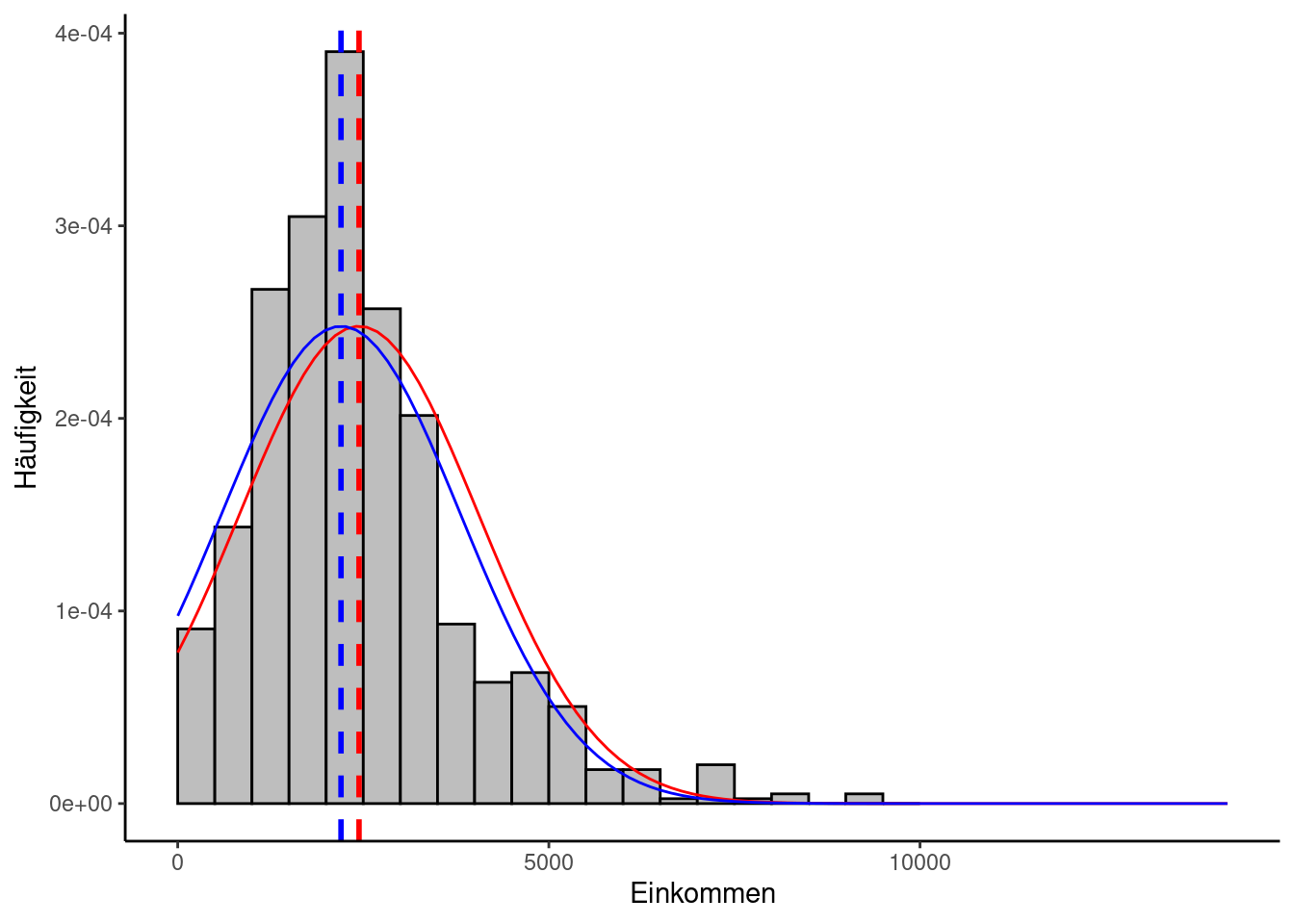
Man sieht darin zweierlei: Zum einen gibt es zwar eine gewisse Übereinstimmung, aber doch auch deutliche Unterschiede zwischen den Messwerten und der Normalverteilung und zum zweiten wirken Median und geometrisches Mittel etwas genauer als das arithmetische Mittel. Hier zeigt sich die stärkere Robustheit des Medians gegenüber Ausreißern.
3.3 Überprüfung der Normalverteilung Q-Q-Plot
Eine andere Möglichkeit, die Daten mit visuellen Methoden auf Normalverteilung zu prüfen, ist ein sogenannter Q-Q-Plot. Dabei werden die Quantile der theoretischen Verteilung auf einer Achse aufgetragen und die dazu korrespondierenden Quantile der empirischen Daten auf der anderen. Sind die Daten normalverteilt, sollten die Punkte im Plot alle sehr dicht an einer gemeinsamen Linie liegen. Glücklicherweise gibt es auch für diesen Plot eine Funktion:
qqnorm(allbus_df$Einkommen) # Erstellen des Q-Q-Plots
qqline(allbus_df$Einkommen) # Einfügen der Linie, auf der die Punkte liegen sollten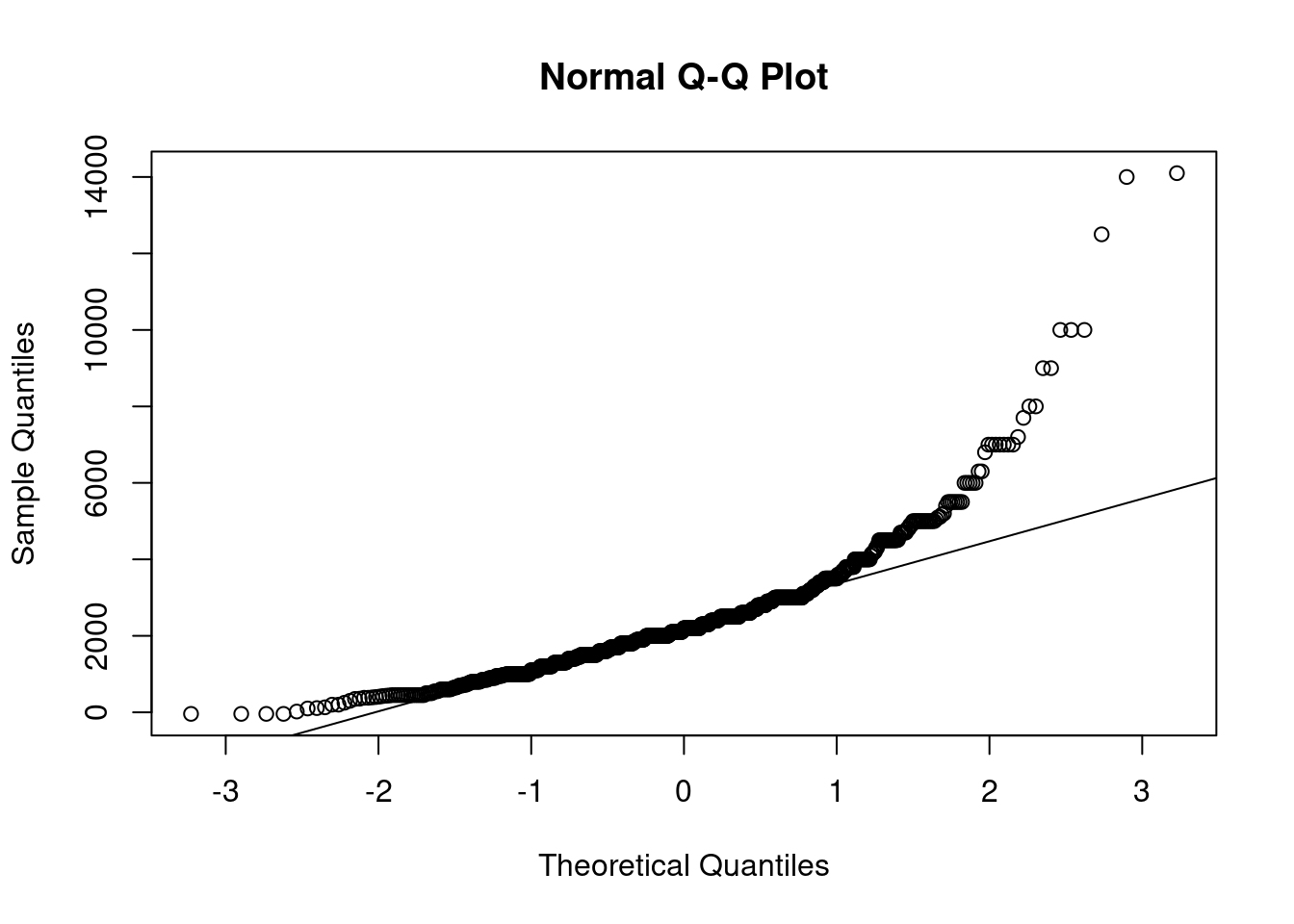
Wie leicht zu sehen ist, weichen die Daten sehr stark von der Linie ab. Der Bereich unterhalb von ca. 3000 Euro Einkommen scheint zumindest teilweise als normalverteilt interpretierbar zu sein, während für höhere Werte die Ergebnisse massiv abweichen. Allerdings muss auch dazugesagt werden, dass ab 5000 Euro aufwärts die Anzahl an Messwerten deutlich abnimmt.
3.4 Überprüfung der Normalverteilung mit stat. Testverfahren
Eine weitere Möglichkeit, auf Normalverteilung zu testen, sind der Kolmogorov-Smirnov-Test und der Shapiro-Wilk-Test. Diese gehen von der Null-Hypothese aus, dass die Daten normalverteilt sind. Wenn der p-Wert also nahe bei 1 liegt, kann man davon ausgehen, dass die Hypothese bestätigt ist. Wenn der p-Wert gegen 0 geht, deutet das darauf hin, dass die Daten nicht normalverteilt sind. Allerdings sind beide Verfahren nicht unproblematisch, da sie mit zunehmender Stichprobengröße immer anfälliger für Ausreißer werden und die Null-Hypothese eher ablehnen. Der Shapiro-Wilk-Test wird vor allem bei kleinen Stichproben (n < 50) eingesetzt.
Zur Demonstration der R-Funktionalitäten sind die beiden Tests hier aufgeführt, wobei die Größe der Stichprobe eine Ablehnung der Null-Hypothese erwarten lässt. Zunächst der Kolmogorov-Smirnov-Test. Es werden an die Funktion übergeben: Die Stichprobe, die Art der Verteilung, auf die getestet werden soll (hier: die Normalverteilung), der Mittelwert sowie die Standardabweichung der Stichprobe:
Asymptotic one-sample Kolmogorov-Smirnov test
data: allbus_df$Einkommen
D = 0.14579, p-value = 3.409e-15
alternative hypothesis: two-sidedDie Warnung macht uns darauf aufmerksam, dass manche Messwerte im Datensatz mehrfach vorkommen. Der p-Wert ist extrem klein, es wird also angenommen, dass die Daten nicht normalverteilt sind.
Analog dazu der Shapiro-Wilk-Test:
Shapiro-Wilk normality test
data: allbus_df$Einkommen
W = 0.83575, p-value < 2.2e-16Auch hier ist der p-Wert extrem klein, weshalb auch hier die Annahme abgelehnt wird, dass die Daten normalverteilt sind.
Um die Problematik dieser beiden Tests zu demonstrieren, wird im folgenden Code-Beispiel eine kleine zufällige Teil-Stichprobe aus dem Einkommens-Datensatz gezogen. Führen Sie es mehrmals aus und schauen Sie sich an, wie stark der p-Wert schwankt:
sample_einkommen = sample(allbus_df$Einkommen, size=20)
ks.test(sample_einkommen, "pnorm", mean=mean(allbus_df$Einkommen), sd=sd(allbus_df$Einkommen))
Asymptotic one-sample Kolmogorov-Smirnov test
data: sample_einkommen
D = 0.27091, p-value = 0.1062
alternative hypothesis: two-sided
Shapiro-Wilk normality test
data: sample_einkommen
W = 0.86251, p-value = 0.0087024 Exkurs: Was ist schon “normal” - Abweichungen von der Normalverteilung
Wenn die Stichprobe keiner Normalverteilung folgt, hat man mehrere Möglichkeiten: Man kann zum einen versuchen, die Daten zu normalisieren, also so zu transformieren, dass sie einer Normalverteilung ähnlicher werden, man kann eine Verteilung wählen, die besser zu den Daten passt und man kann auf Methoden ausweichen, die keine Normalverteilung voraussetzen.
Das folgende Code-Beispiel zeigt eine R-Funktion, die einem helfen kann, eine passende Verteilung zu finden. Sie orientiert sich an den Eigenschaften Schiefe (Skewness) und Wölbung (Kurtosis). Die Schiefe haben wir bereits kennengelernt. Die Wölbung gibt an, wie flach eine Verteilung ist. Wir haben es mit kontinuierlichen Werten zu tun, also setzen wir “discrete” auf FALSE:
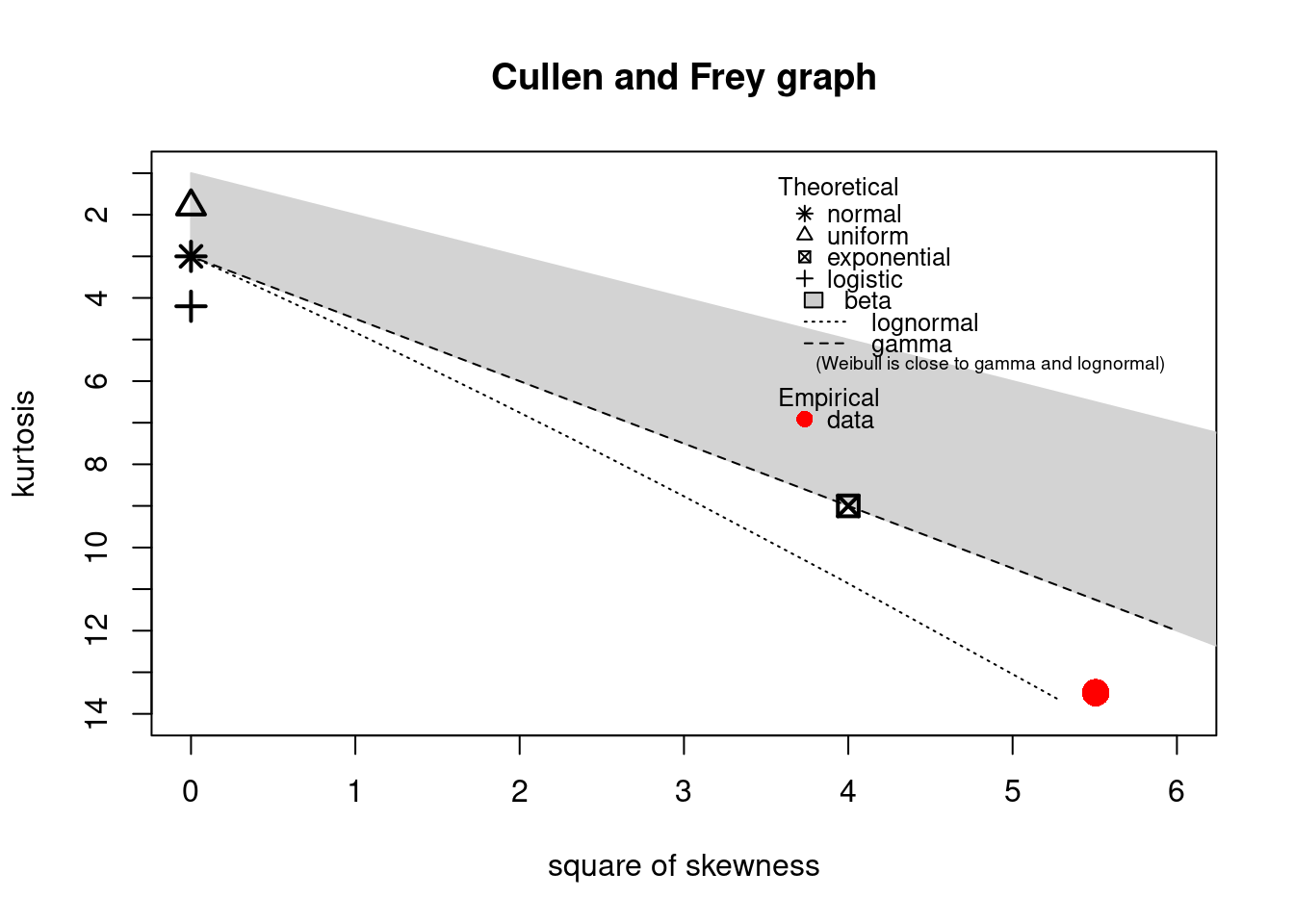
summary statistics
------
min: -41 max: 14100
median: 2200
mean: 2442.545
estimated sd: 1609.459
estimated skewness: 2.346469
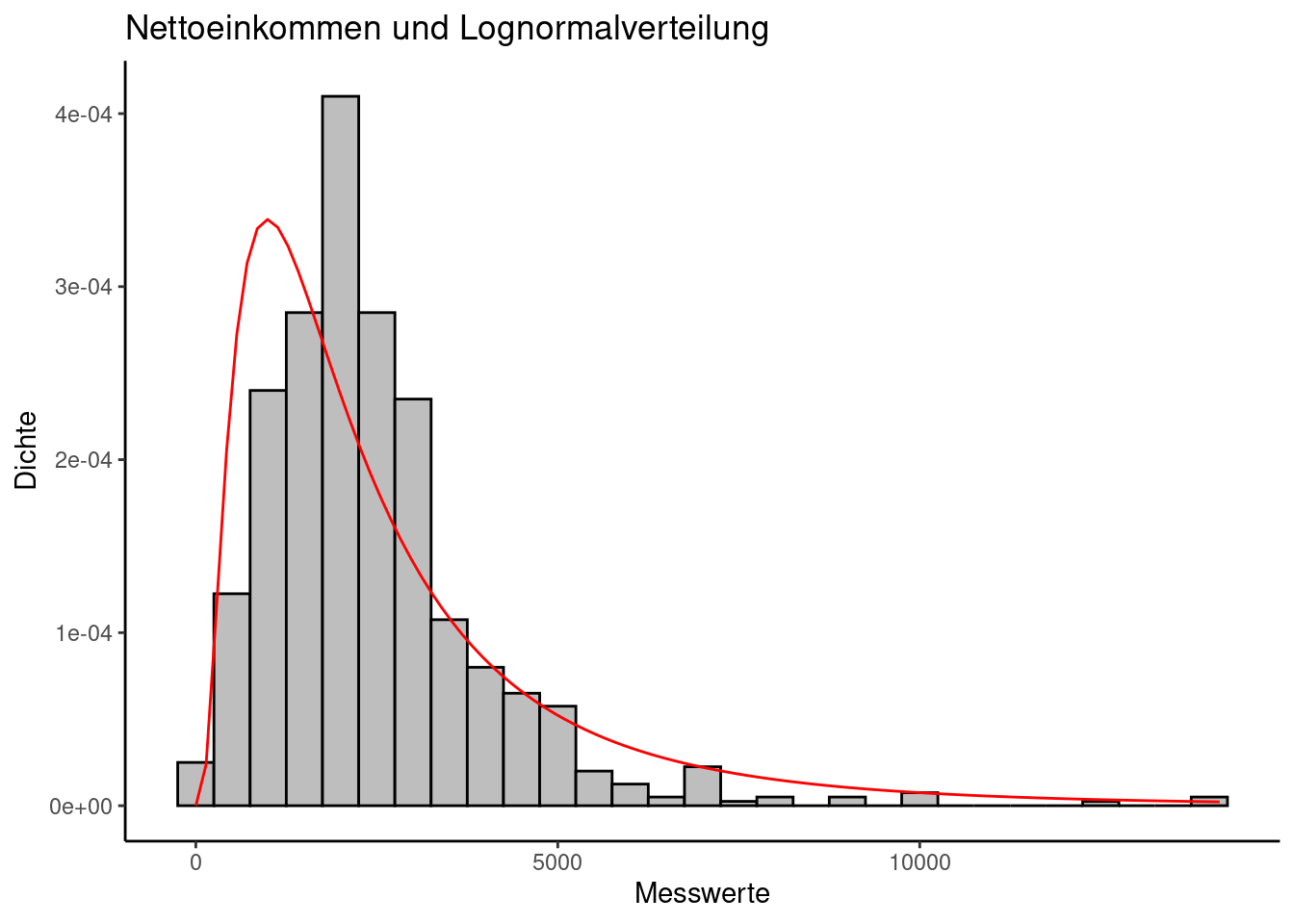
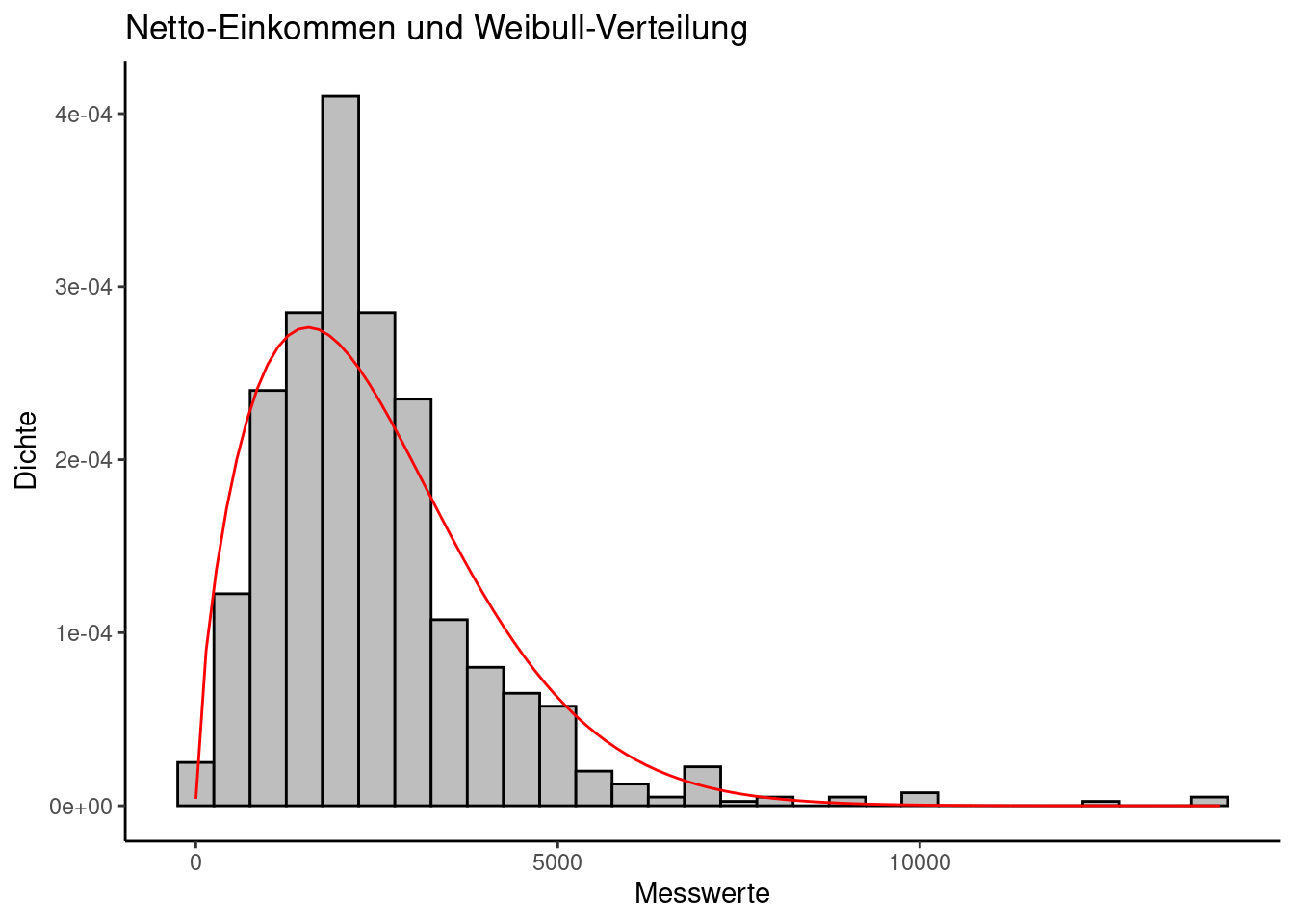
estimated kurtosis: 13.49052 Der blaue Punkt gibt an, wo sich die Verteilung unserer empirischen Daten befindet. Er liegt sehr nahe an der Lognormalverteilung, aber auch die Weibull-Verteilung könnte ein passender Kandidat sein.
Wir haben diese Verteilung bereits angesprochen. Für Daten, die einen natürlichen Nullpunkt haben, ist die Lognormalverteilung ein möglicher Kandidat, weil sie nicht symmetrisch ist wie die Normalverteilung. Zur Normalisierung ist sie sehr nützlich. Allerdings sollte man daran denken, dass sie nur mit Werten funktioniert, die größer als Null sind. Man muss also ggf. die Messwerte vorher anpassen.
Die Formel ähnelt der für die Normalverteilung:
\[ f(x;\mu,\sigma) = \frac{1}{x \cdot \sigma \sqrt{2\pi}} \cdot e^{-\frac{(\ln(x)-\mu)^2}{2\sigma^2}} \]
Schauen wir uns einmal an, wie unsere Einkommensdaten zur Dichtefunktion der Lognormalverteilung passen. Dazu addieren wir zunächst zu jedem Messwert die Zahl 42, damit alle Werte größer Null sind, logarithmieren dann die Messwerte und ermitteln anschließend das arithmetische Mittel und die Standardabweichung:
log.allbus.df = data.frame(LogEinkommen=log(allbus_df$Einkommen + 42))
log.mean = mean(log.allbus.df$LogEinkommen)
log.sd = sd(log.allbus.df$LogEinkommen)
cat("Mittelwert: ", log.mean, "Standardabweichung: ", log.sd)Mittelwert: 7.598287 Standardabweichung: 0.8396802Dann plotten wir das Ergebnis in einem Histogramm, in das wir die theoretische Dichte der Lognormalverteilung eintragen, die unseren Parametern entspricht:
ggplot(data = allbus_df, aes(x=Einkommen + 42)) +
geom_histogram(aes(y=..density..), binwidth = 500, fill = "gray", color = "black") +
labs(
title = "Nettoeinkommen und Lognormalverteilung", x = "Messwerte", y = "Dichte") +
stat_function(fun=dlnorm, args=list(meanlog=log.mean, sdlog=log.sd), colour="red") #meanlog=log.mean, sdlog=log.sd
Die theoretische Verteilung wirkt schiefer als die empirische, aber insgesamt scheint die Übereinstimmung auch visuell größer zu sein als mit der Normalverteilung.
Der zweite Kandidat, der sich bei stetigen, asymmetrischen Verteilungen anbieten kann, ist die Weibull-Verteilung. Sie ist sehr vielseitig, bezogen auf die Formen, die sie annehmen kann und wird deshalb oft für die Kalkulation der Lebensdauer von Maschinenteilen u.ä. verwendet. Allerdings kann sie auch bei der Untersuchung von Einkommensungleichheiten von Bedeutung sein.
Diese Verteilung ist abhängig von einem Streuungsparameter \(1 / \lambda\) und dem Formparameter \(k\):
\[ f(x;\lambda,k) = \frac{k}{\lambda} \left(\frac{x}{\lambda}\right)\^{k-1} e^{-(x/^\lambda)k} \]
Durch den Parameter \(k\) kann man berücksichtigen, wie sich die Häufigkeit, mit der ein bestimmtes Ereignis auftritt, verändert. Wenn \(k = 1\), geht man davon aus, dass sich die Wahrscheinlichkeit, dass ein Ereignis eintritt, kaum verändert. Für \(k < 1\) erwartet man, dass Ereignisse über die Zeit seltener auftreten und für \(k > 1\), dass sie mit der Zeit zunehmen.
Auf den Netto-Einkommens-Datensatz angewendet, ergibt sich ein Bild, das wie erwartet ähnlich wie die Lognormal-Verteilung wirkt, wenn auch immer noch mit deutlichen Abweichungen.
fit.weibull = fitdist(allbus_df$Einkommen + 42, "weibull")
ggplot(data = allbus_df, aes(x=Einkommen + 42)) +
geom_histogram(aes(y=..density..), binwidth = 500, fill = "grey", color = "black") +
labs(
title = "Netto-Einkommen und Weibull-Verteilung",
x = "Messwerte",
y = "Dichte"
) +
stat_function(fun=dweibull, args=list(scale=fit.weibull$estimate["scale"], shape=fit.weibull$estimate["shape"]), colour="red")